Question

Пожалуйста решение с рисунками. 1) Сколько ребер, граней, вершин имеет 14-угольная призма?2) Стороны основания прямоугольного параллелепипеда равны 6 см и 9 см, а диагональ равна 11 см. Найдите площадь полной поверхности параллелепипеда.3) Сторона основания правильной треугольной призмы равна 6 см. Через сторону основания призмы проведено сечение, которое образует угол 60° с плоскостью основания и пересекает боковое ребро. Найдите площадь этого сечения.​

Answer 1

Объяснение:

1)

сколько граней, ребер, вершин у призмы можно узнать с помощью формул(n - число сторон многогранника)

Количество граней равно n+2 ,где

n - боковые грани , 2 - основание призмы.

Количество ребер равно 3n.

Количество вершин равно 2n

14 -угольная призма:

Количество граней равно 14+2=16

Количество ребер равно 3•14=42

Количество вершин рано 2•14=28

2)

АВСDA1B1C1D1 - прямоугольный параллелепипед;

сторона а=9 см

сторона b=6 см

диагональ d=11 cм

Sпол поверх=?

Sполн. поверх=2•а•b+2•a•c+2•b•c

d²=a²+b²+c²

c=√(d²-a²-b²)=√(11²-9²-6²)=√4=2 см

Sполн поверх=2•9•6+2•9•2+2•6•2=

=108+36+24=168 см²

ответ: 168 см²

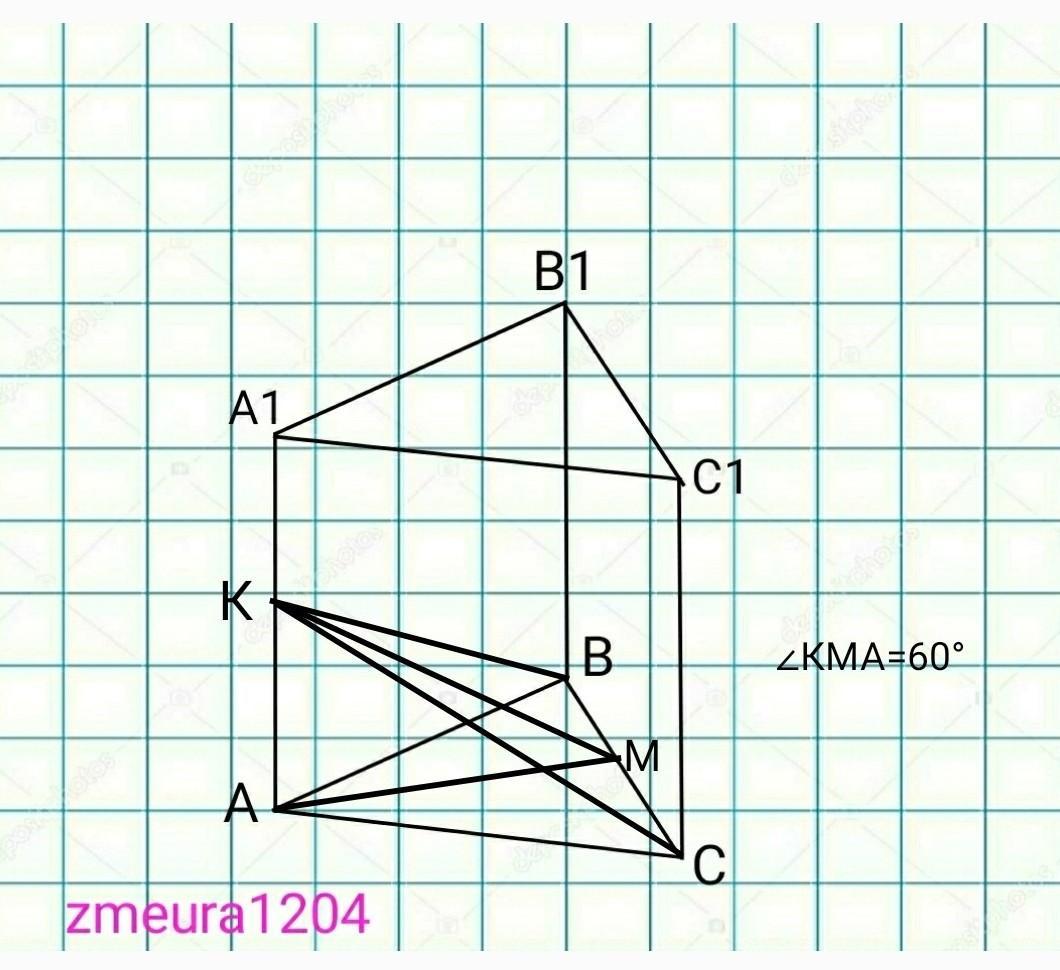
3)

АВСА1В1С1 - правильная треугольная призма

АВ=ВС=АС=6 см

ВСК - сечение

∠АНК=α=60°

найти : S(BCK)

решение:

АН проекция КН, КН⟂ВС, АН - медиана ,высота.

∆АВС - равносторонний:

АН=ВС•√3/2=6•√3/2=3√3 см.

∆КАН - прямоугольный:

cosa=AH/KH;

KH=AH/cosa=(3√3)/cos60=3√3/(1/2)=6√3 см

S(BCK)=1/2•BC•KH=1/2•6•6√3=18√3 см²

ответ: 18√3 см²

Answer 2

Объяснение:

1) 14- ребер в нижнем основании; 14-ребер в боковой поверхности; 14- ребер в верхнем основании. Всего: 14*3=32ребра.

...........

14- граней в боковой поверхности, 2- грани основания. Всего: 14+2=16 граней.

...........

14- вершин в верхнем основании, и 14- вершин в нижнем. Всего: 28 вершины.

________________

2)

АВ=СD=6см

ВС=АD=9см

А1С=11см

∆АВС- прямоугольный треугольник

По теореме Пифагора:

АС²=АВ²+ВС²=6²+9²=36+81=117см²

∆АА1С- прямоугольный треугольник

По теореме Пифагора:

АА1=√(А1С²-АС²)=√(11²-117)=

=√(121-117)=√4=2см

Р(ABCD)=2(AB+BC)=2(6+9)=

=2*15=30см

Sб=Р(ABCD)*AA1=30*2=60см²

S(ABCD)=AB*BC=6*9=54см²

Sпов=Sб+2*S(ABCD)=60+2*54=

=168см²

Ответ: Площадь поверхности параллелепипеда равна 168см²

____________

3)

АВ=ВС=АС=6см

∠КМА=60°

АМ- высота, медиана и биссектриса равностороннего треугольника ∆АВС.

АМ=АВ√3/2=6√3/2=3√3см.

∆КАМ- прямоугольный треугольник.

∠КАМ=90°; ∠КМА=60°;

∠АКМ=180°-∠КАМ-∠КМА=

=180°-90°-60°=30°

АМ- катет против угла 30°

КМ=2*АМ=2*3√3=6√3см

S(∆KBC)=½*KM*BC=½*6√3*6=18√3см²

Или решение 2)

S(∆ABC)=S(∆KBC)*cos∠KMA; →

S(∆KBC)=S(∆ABC)/cos60°;

S(∆ABC)=AB²√3/4=6²√3/4=9√3см²

S(∆KBC)=9√3/½=9√3/1*2/1=18√3см²

Ответ: площадь сечения равна 18√3см²

Answer 3

1) Для определения количества рёбер, граней и вершин в 14-угольной призме, давайте разберёмся с её структурой.

14-угольная призма имеет две основы и 14 граней боковых сторон. Поскольку каждая из этих граней прямоугольник, то она имеет 4 стороны. Таким образом, всего боковых рёбер: 14 граней x 4 стороны = 56 боковых рёбер.

Каждая основа призмы - это 14-угольник, который имеет 14 сторон. Поэтому у нас есть две основы, и общее количество рёбер на основах: 2 основы x 14 сторон = 28 рёбер на основах.

Теперь найдем количество вершин. Вершины призмы соответствуют точкам пересечения рёбер. Вершины на каждой из двух основ призмы равны числу углов в 14-угольнике, то есть 14 вершин на каждой основе. Однако две из этих вершин являются общими для обеих основ. Поэтому общее количество вершин: 14 вершин на каждой основе + 14 вершин на другой основе - 2 общие вершины = 26 вершин.

Итак, для 14-угольной призмы: - Количество рёбер: 56 (боковых) + 28 (на основах) = 84 ребра. - Количество граней: 14 (боковых) + 2 (основы) = 16 граней. - Количество вершин: 26 вершин.

2) Для нахождения площади полной поверхности прямоугольного параллелепипеда, нам понадобятся его стороны и диагональ.

Стороны основания параллелепипеда равны 6 см и 9 см. Площадь одной из этих сторон (прямоугольника) равна: Площадь = Длина x Ширина = 6 см x 9 см = 54 см²

Параллелепипед имеет 6 таких одинаковых граней, поэтому общая площадь его поверхности равна: Площадь поверхности = 6 x (Площадь одной грани) = 6 x 54 см² = 324 см²

Итак, площадь полной поверхности прямоугольного параллелепипеда равна 324 квадратным сантиметрам.

3) Для нахождения площади сечения правильной треугольной призмы, проведенного плоскостью, образующей угол 60° с плоскостью основания и пересекающего боковое ребро, давайте рассмотрим эту ситуацию:

Сначала найдем высоту сечения, которая является одной из сторон треугольника. Эта высота равна половине высоты призмы. Так как сторона основания призмы равна 6 см, а угол между плоскостью сечения и плоскостью основания равен 60°, то высота сечения составляет (1/2) * 6 см = 3 см.

Теперь рассмотрим равносторонний треугольник, образованный сечением призмы. У нас есть сторона треугольника равная 6 см и высота равная 3 см. Мы можем использовать формулу для площади равностороннего треугольника:

Площадь = (сторона^2 * √3) / 4

Подставляя значения, получим: Площадь = (6 см^2 * √3) / 4 = (36√3) / 4 = 9√3 квадратных сантиметра.

Итак, площадь сечения треугольной призмы равна 9√3 квадратных сантиметров.