Question

Три станка производят соответственно 50%, 30% и 20% всех изделий. В их продукции брака составляет соответственно 1%, 2% и 1,5%. Какова вероятность того, что выбранное наугад бракованное изделие было изготовлено на втором станке?

Answer 1

Пусть событие А состоит в том, что бракованное изделие было изготовлено на втором станке.

Рассмотрим гипотезы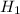  $H_1$,  $H_2$ и $H_3$.
$H_1~-~ \{$ изделие изготовлено первым станком. $\}$
$H_2~-~ \{$ изделие изготовлено вторым станком. $\}$
$H_3~-~ \{$ изделие изготовлено третьим станком. $\}$

Условные вероятности того, что продукции брака составляют 
$P_{H_1}(A)=0.01;~~~ P_{H_2}(A)=0.02;~~~P_{H_3}(A)=0.015$

Искомая вероятность по формуле Байеса:

$P_A(H_2)= \dfrac{P(H_2)\cdot P_{H_2}(A)}{P(H_1)P_{H_1}(A)+P(H_2)P_{H_2}(A)+P(H_3)P_{H_2}(A)} =\\ \\ \\ = \dfrac{0.3\cdot0.02}{0.5\cdot0.01+0.3\cdot 0.02+0.2\cdot0.015} =\dfrac{0.006}{0.014}=\dfrac{3}{7} \approx0.43$

Answer 2

Давайте решим эту задачу, используя формулу условной вероятности.

Пусть:

• A - событие "изделие бракованное"
• B - событие "изделие изготовлено на втором станке"

Мы хотим найти вероятность P(B|A), то есть вероятность того, что изделие было изготовлено на втором станке при условии, что оно бракованное.

Из условия задачи у нас есть следующая информация:

• P(A|B) = 0.02 (вероятность того, что изделие будет бракованным, если оно изготовлено на втором станке)
• P(A) = 0.010.3 + 0.020.5 + 0.015*0.2 = 0.0095 + 0.01 + 0.003 = 0.0225 (вероятность появления бракованного изделия)

Теперь мы можем использовать формулу условной вероятности: P(B|A) = P(A|B) * P(B) / P(A)

P(B) - вероятность того, что выбранное наугад изделие было изготовлено на втором станке, равна 0.3.

Теперь подставим все значения в формулу:

P(B|A) = 0.02 * 0.3 / 0.0225 = 0.06 / 0.0225 = 2.67

Таким образом, вероятность того, что выбранное наугад бракованное изделие было изготовлено на втором станке, составляет 2.67% (или около того).