
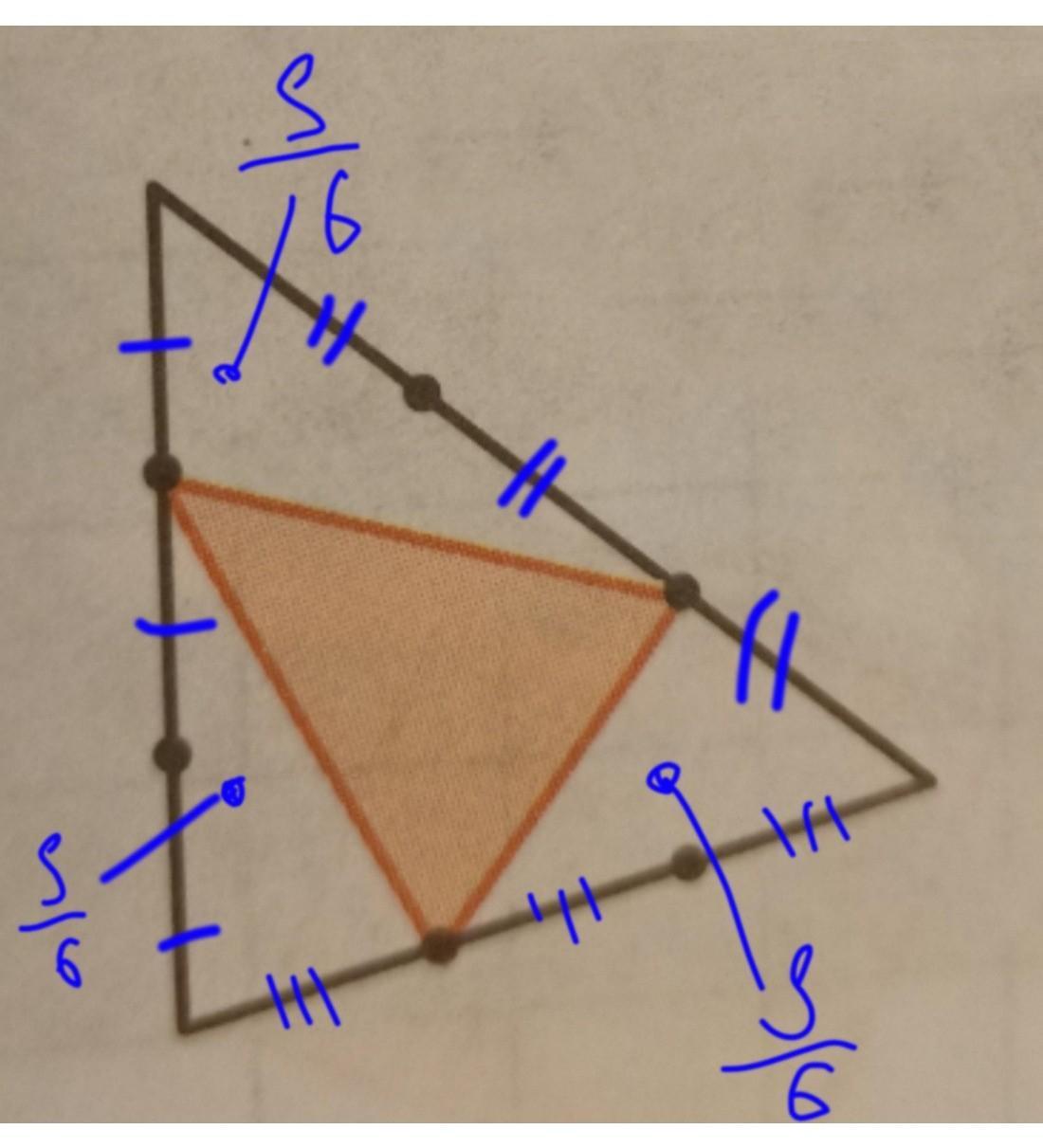
Площадь треугольника равна 1.Каждая его сторона отмеченными точками делится на равные части.
Найдите площади закрашенных фигур на рисунке.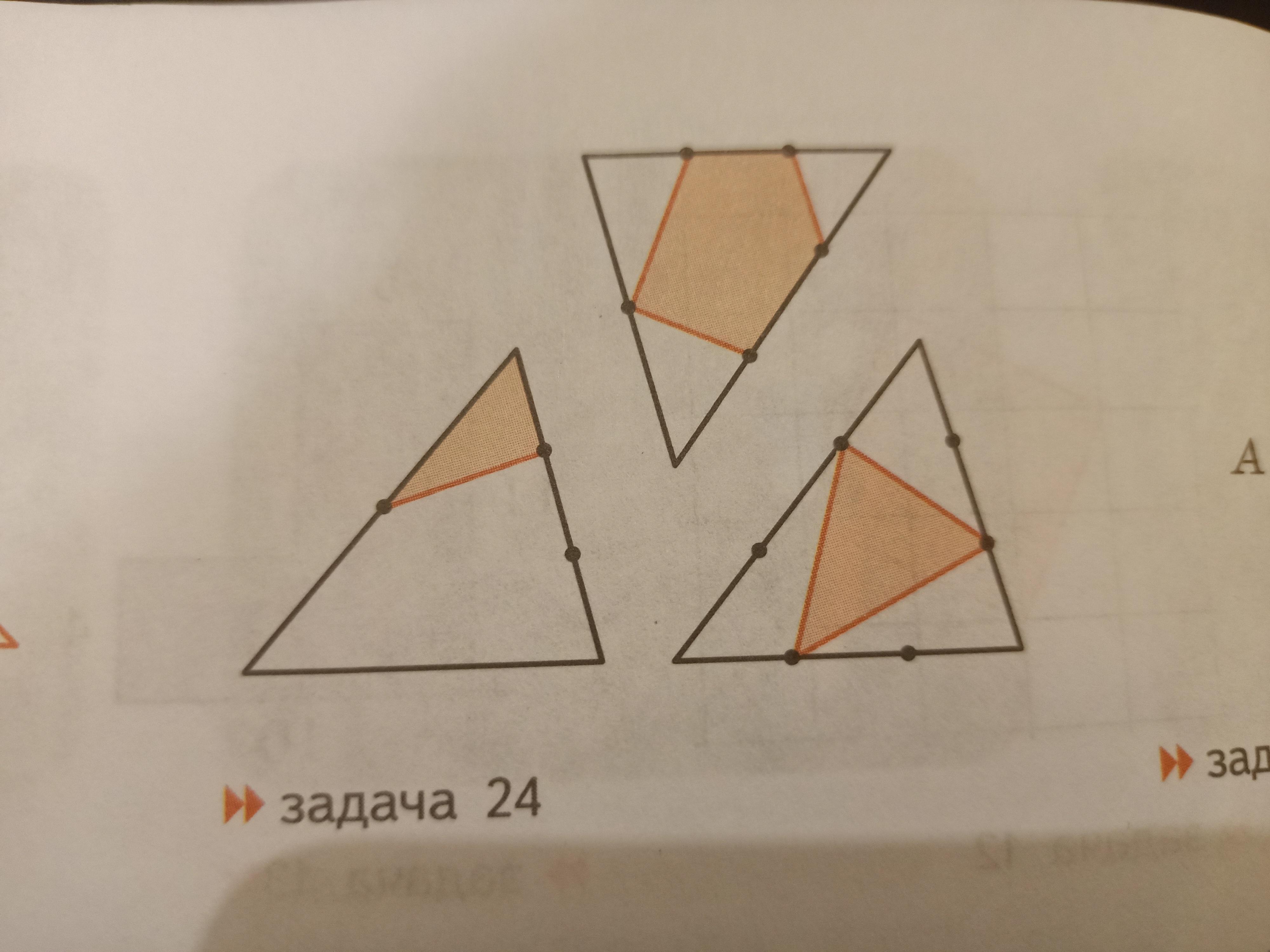

 0
0
 0
0
Ответы на вопрос
 Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.
Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.

Ответ:
1) S = 1/6
2) S = 1/2
3) S = 5/9
Объяснение:
Площадь треугольника можно вычислить по следующей формуле:
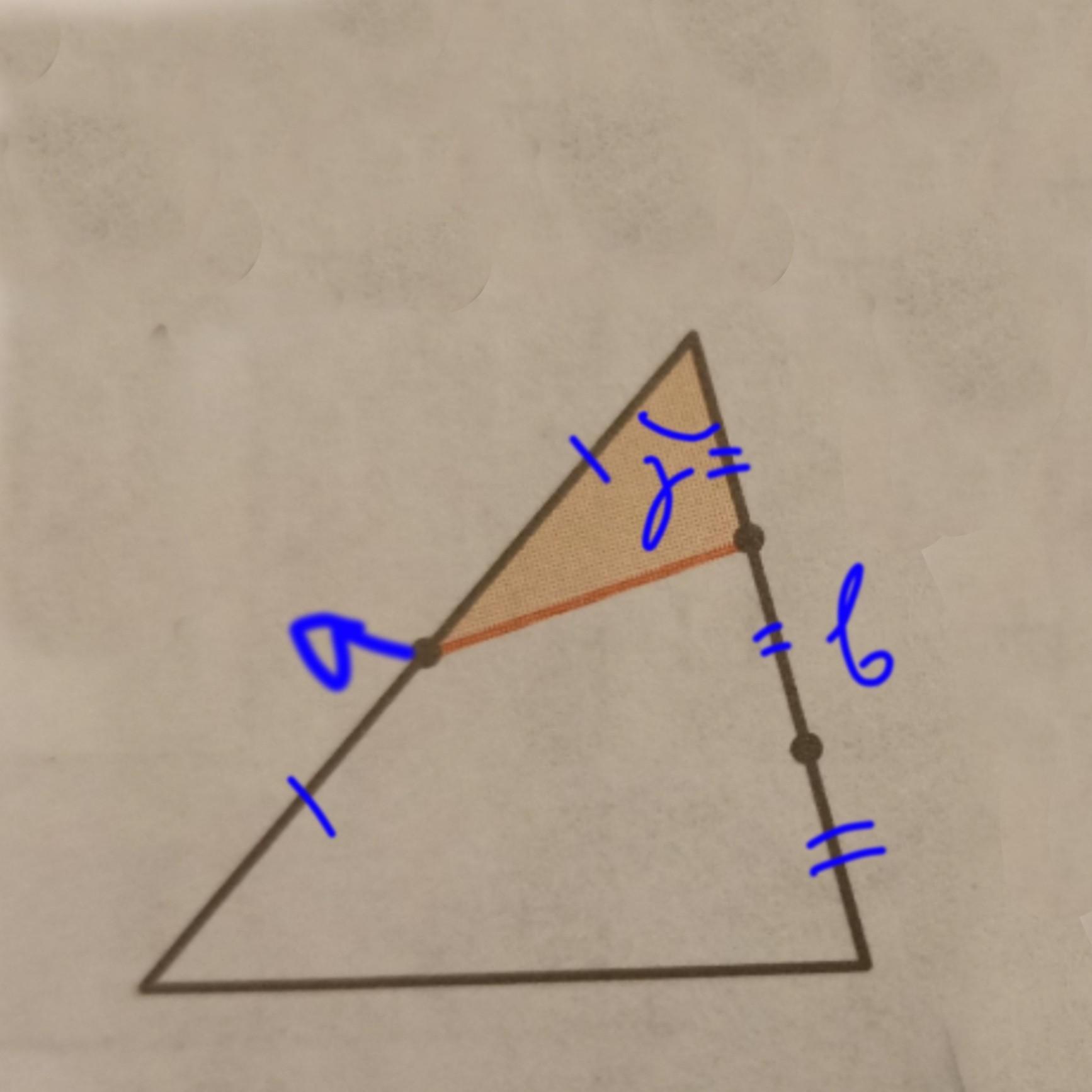
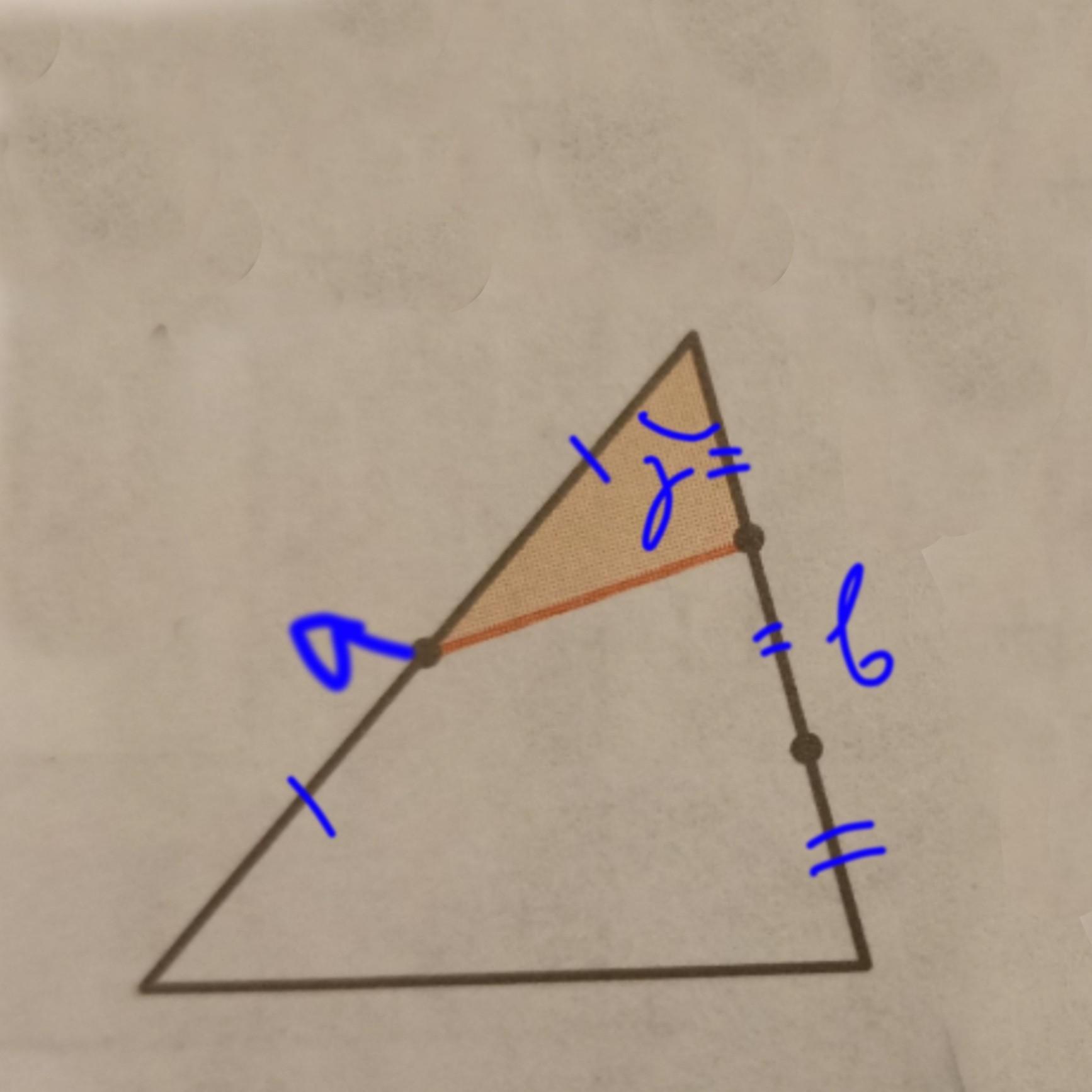
1) Обозначим площадь закрашенного ∆-ка S1 (см. рис.1)
Очевидно, т.к. точки делят стороны "единичного" ∆ка на равные отрезки, а угол у единичного и у малого треугольника общий, то
и площадь S1 равна
А т.к.
2) Пусть площадь закрашенной фигуры (а это - треугольник, см. рис.) равна S1.
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (обозначим их площади S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Треугольники 2, 3, 4 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Соответственно, искомая площадь составляет
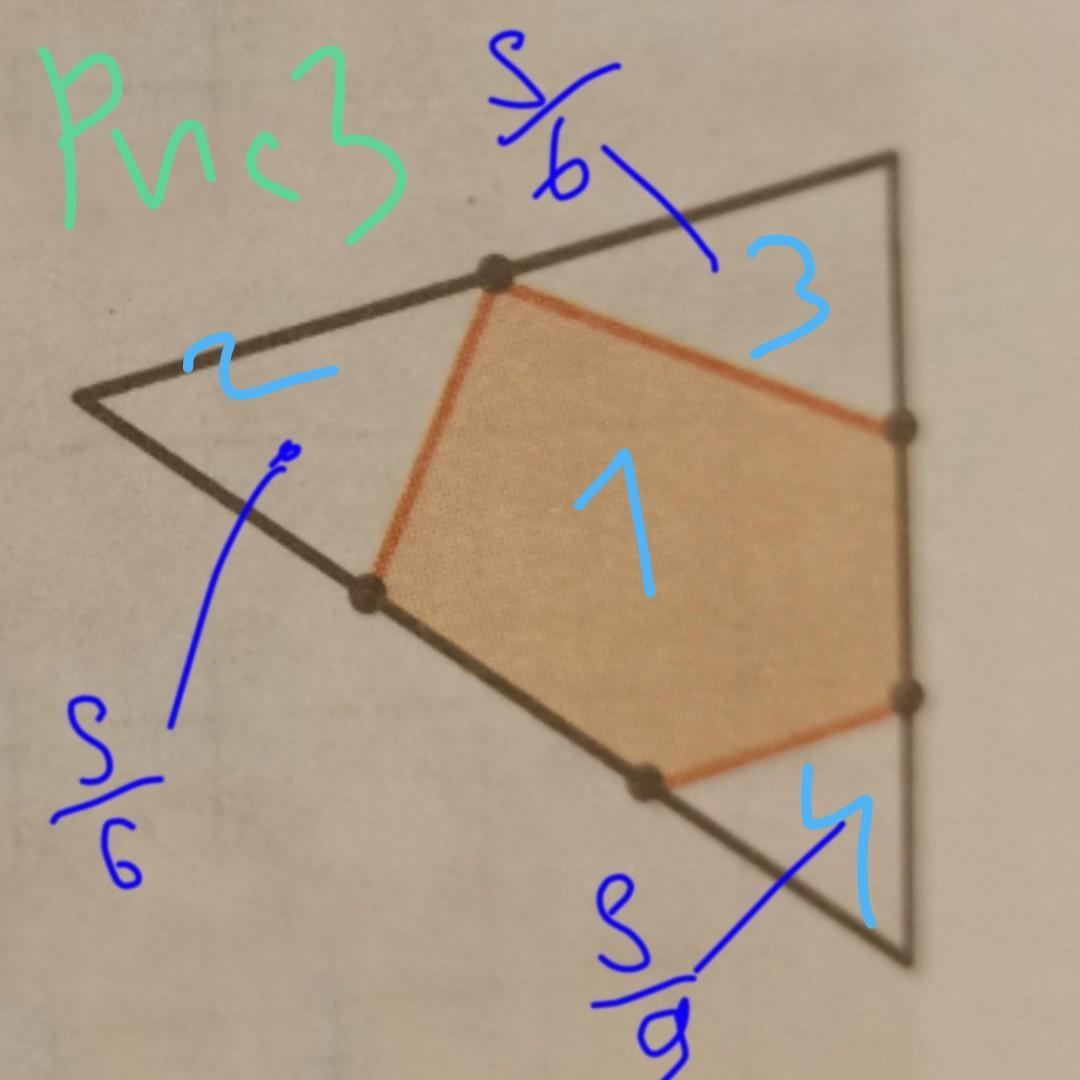
3) Пусть площадь закрашенной фигуры (а это - шестиугольник, см. рис.) равна S1
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (пусть их площади будут S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
Площади треугольников 2, 3 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
Но площадь треугольника 4 меньше: у него две стороны втрое меньше чем у исходного единичного, потому его площадь равна:
Следовательно, общая площадь незакрашенных частей равна:
А искомая площадь закрашенной фигуры S1 составляет

 0
0
 0
0
Топ вопросов за вчера в категории Геометрия





Последние заданные вопросы в категории Геометрия
-
Математика
-
Литература
-
Алгебра
-
Русский язык
-
Геометрия
-
Английский язык
-
Химия
-
Физика
-
Биология
-
Другие предметы
-
История
-
Обществознание
-
Окружающий мир
-
География
-
Українська мова
-
Информатика
-
Українська література
-
Қазақ тiлi
-
Экономика
-
Музыка
-
Право
-
Беларуская мова
-
Французский язык
-
Немецкий язык
-
МХК
-
ОБЖ
-
Психология
-
Физкультура и спорт
-
Астрономия
-
Кыргыз тили
-
Оʻzbek tili













