Question

высота правильной треугольной пирамиды равна а√3, радиус окружности, описанной около её основания, равен 2а. Найдите:a) апофему пирамиды; б) угол между боковой гранью и основанием;b) площадь боковой поверхности.​​

Answer 1

Объяснение:

удачи солнце

хорошего дня , и возможно каникул

Answer 2

Ответ:

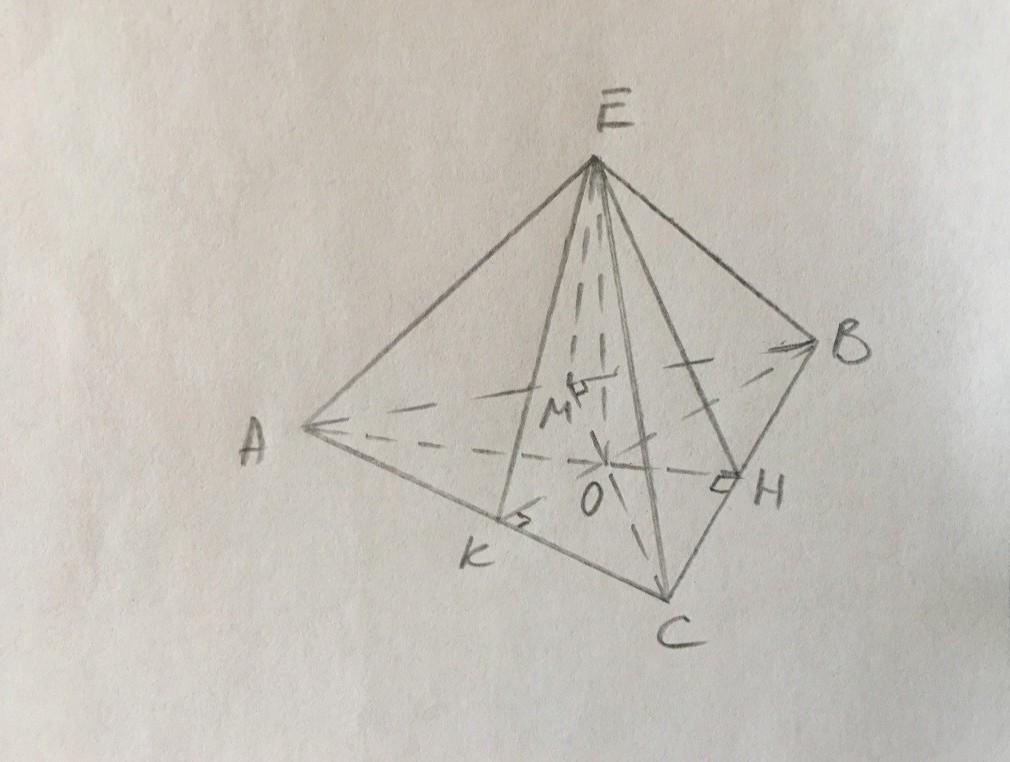
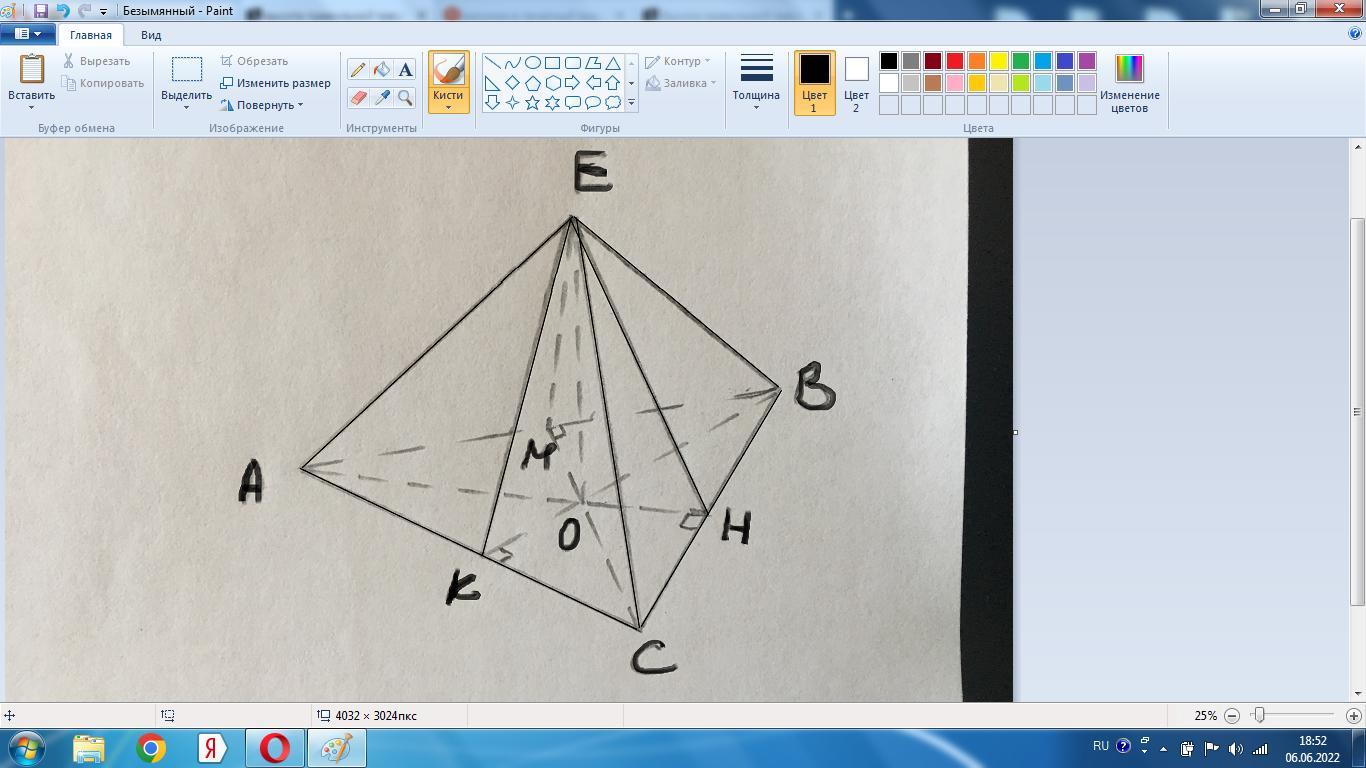
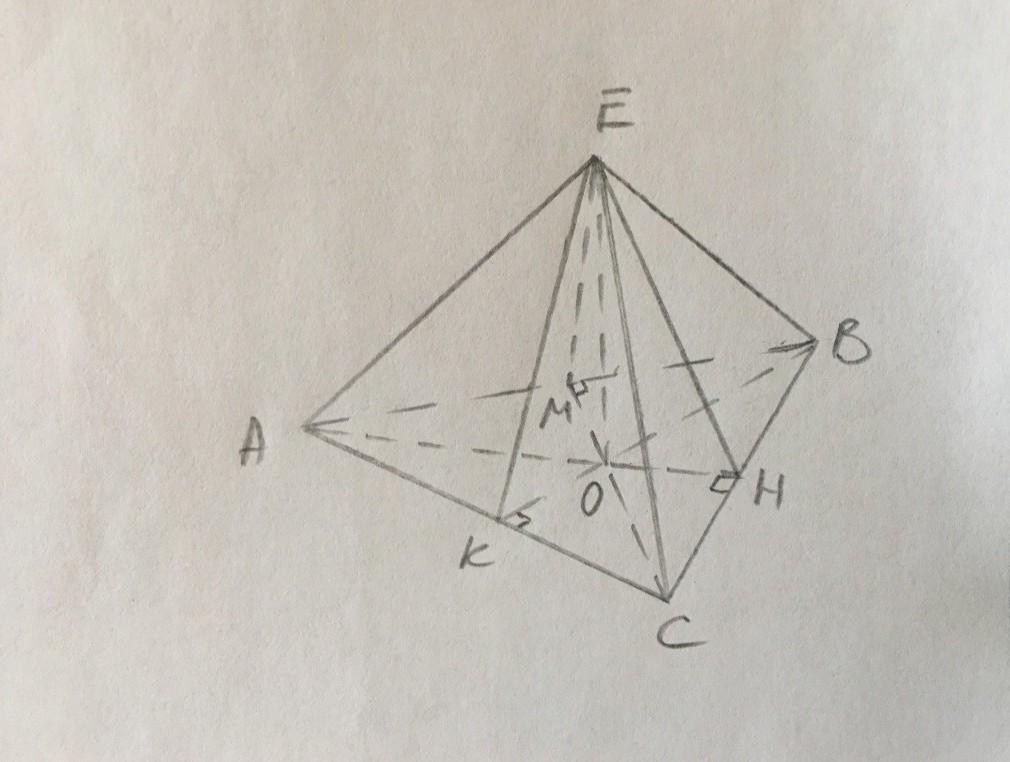
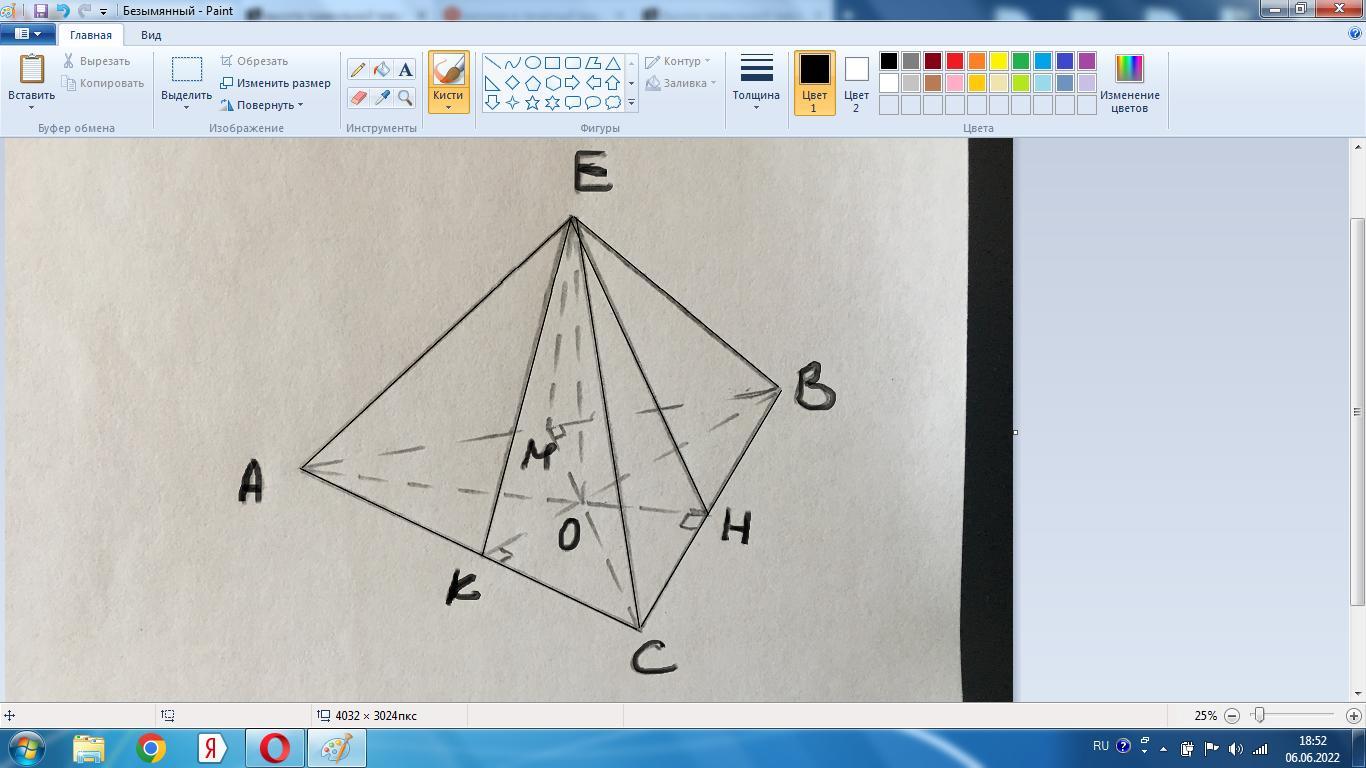
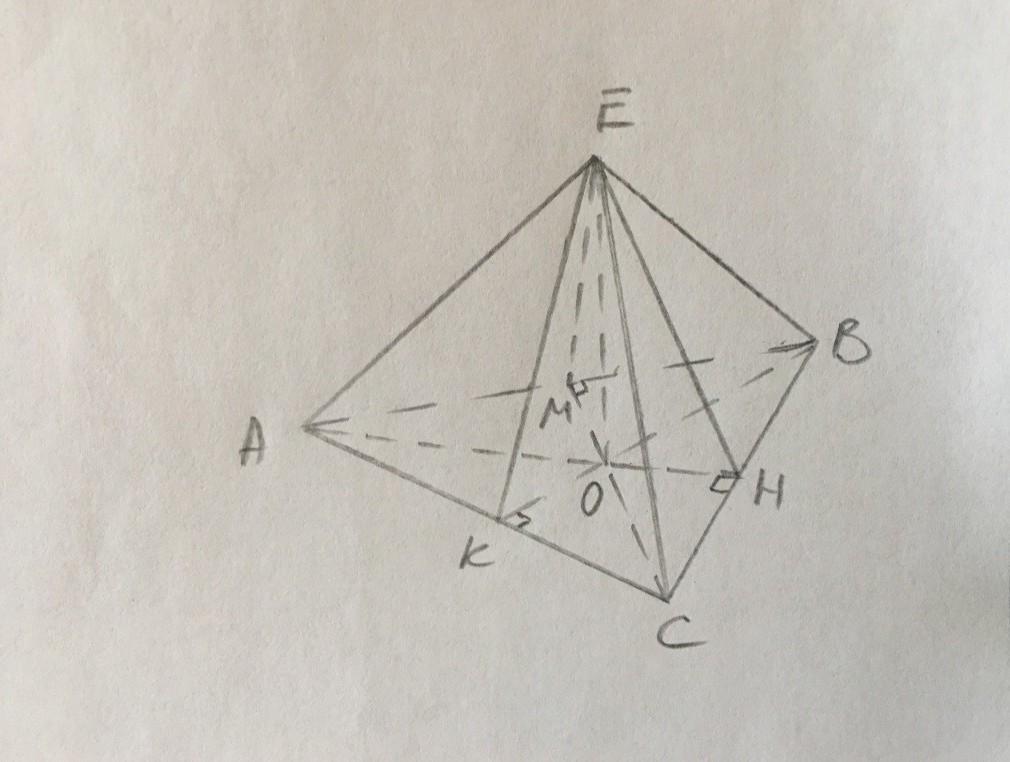
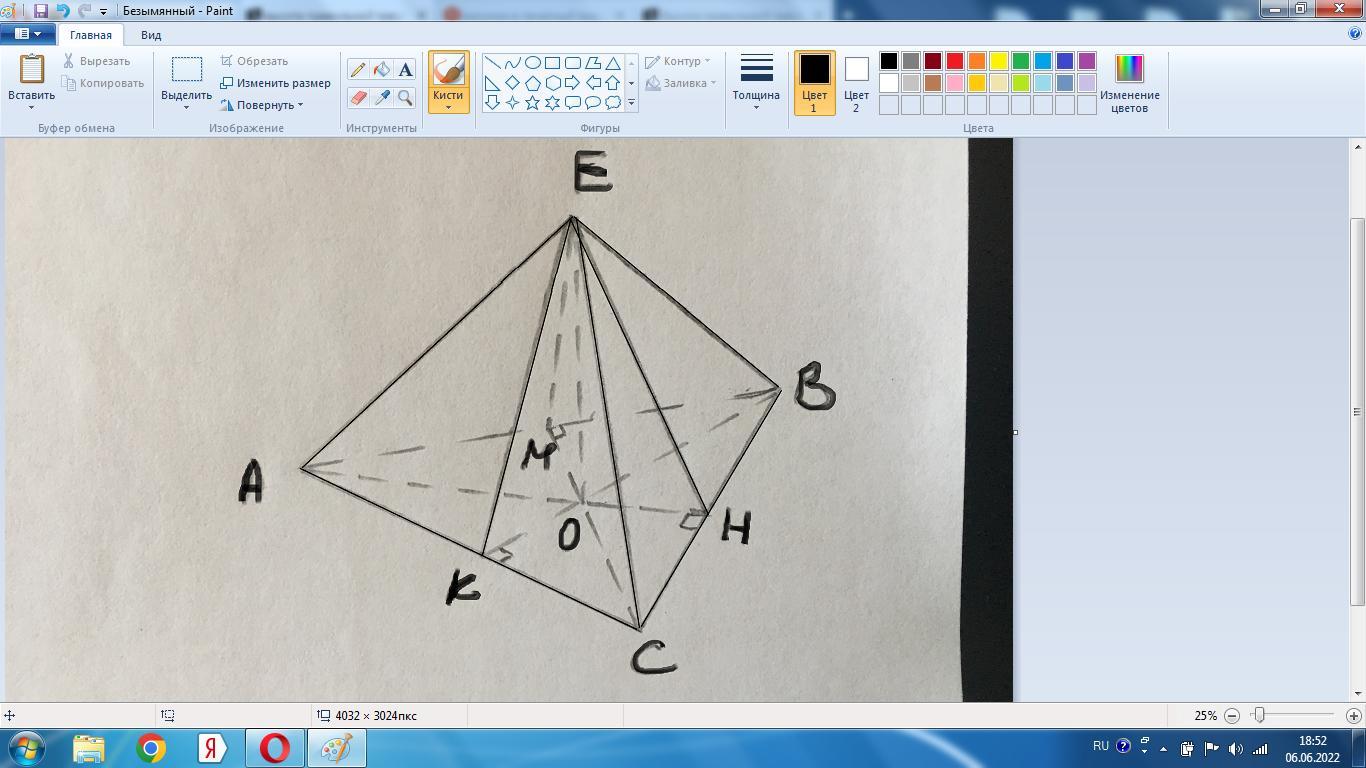
а)АВСЕ - пирамида с вершиной Е.

В основании лежит правильный Δ, для которого радиус описанной окружности равен r=R/2.

ОК=ОВ/2=2а/2=а.

В Δ ЕКО найдем апофему ЕК:

ЕК²=ЕО²+ОК²=3а²+а²=4а²,

ЕК=2а - апофема.

б) ЕК/ОК=2а/а=2. В прямоугольном Δ ЕОК гипотенуза ЕК в 2 раза больше катета ОК, получается ∠КЕО=30°.

Тогда ∠ЕКО=60° - угол между боковой гранью и основанием.

в) Площадь боковой поверхности:

Sб=Р*l/2

R=AB/√3

AB=R√3=2a√3.

P=3AB=6a√3.

Sб=6a√3·2a/2=6a²√3 (ед²) - площадь боковой поверхности.