Question

помогите решить ...В прямоугольном треугольнике ABC точка О- середина медианы CH, проведенной к гипотенузе AB, AC=6 см, BC=8 см. Найдите площадь треугольника OBC.

Answer 1

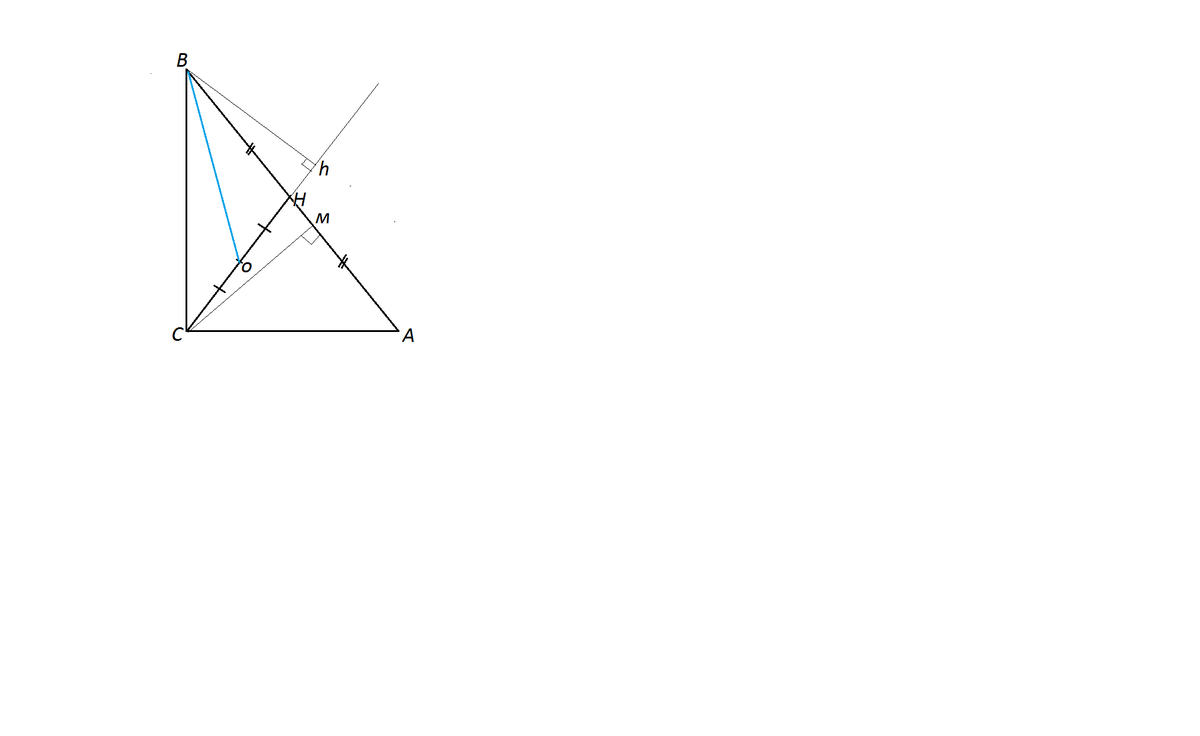
В прямоугольном треугольнике ABC точка О- середина медианы CH, проведенной к гипотенузе AB, AC=6 см, BC=8 см. 
Найдите площадь треугольника OBC.

----------Для решения задачи нужно вспомнить, что медиана делит треугольник на два равновеликих ( т.е. на два треугольника с равной площадью). 
В прямоугольном треугольнике медиана СН разделила его на два треугольника.
 Высота треугольника СВН и САН одна и та же - СМ, а основания равны. 
Следовательно, площадь каждого из этих треугольников равна половине площади треугольника АСВ.
 S ACB=АС*ВС:2=24 см² 
Точно так же медиана ВО треугольника ВСН делит его на два равновеликих треугольника с общей высотой Сh,  и площадь каждого равна половине площади треугольника ВСН и, соответственно, одной четверти площади треугольника АВС. 
Площадь треугольника ОВС равна 24:4=6 см²