Question

ПОМОГИТЕ ПОЖАЛУЙСТА!В остроугольном треугольнике ABC проведены высоты BB1 и CC1. На высоте BB1 выбрана точка D такая, что B1D=C1D. Точка M — середина BC. Найдите величину угла DMC, если ∠B=74∘, ∠C=65∘.

Answer 1

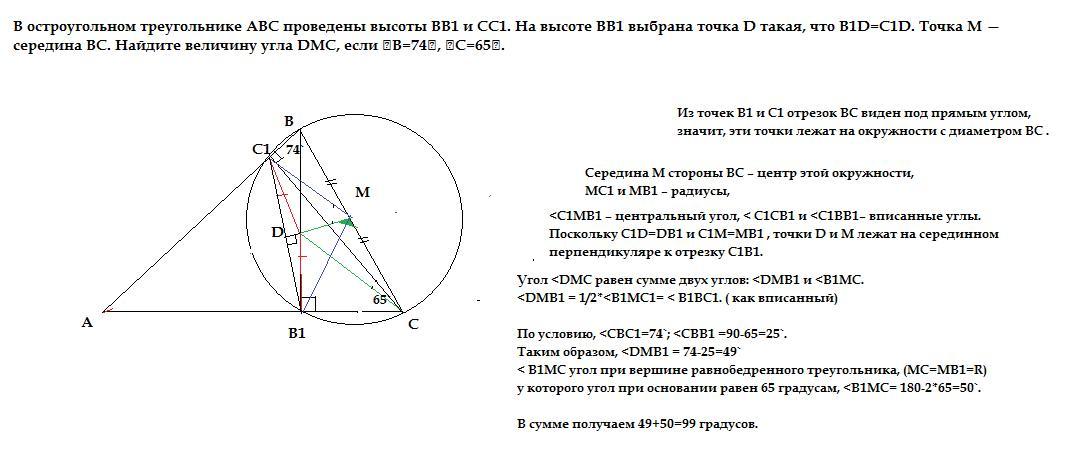
В остроугольном треугольнике ABC проведены высоты BB1 и CC1. На высоте BB1 выбрана точка D такая, что B1D=C1D. Точка M — середина BC. Найдите величину угла DMC, если ∠B=74∘, ∠C=65∘.

Answer 2

Для решения этой задачи давайте следовать следующим шагам:

1. Найдем угол A, используя свойство остроугольного треугольника: A + B + C = 180°. A = 180° - B - C = 180° - 74° - 65° = 41°.

2. Так как BB1 и CC1 - высоты, они перпендикулярны соответственно к AC и AB. Это также означает, что B1D и C1D тоже перпендикулярны к AC и AB. Из этого следует, что треугольники B1DB и C1DC являются прямоугольными.

3. Так как B1D = C1D, и оба треугольника B1DB и C1DC прямоугольные, то эти треугольники равнобедренные. Это означает, что углы B1BD и C1CD равны между собой.

4. Так как BB1 - высота, то BB1 является медианой треугольника ABC. Следовательно, треугольники ABB1 и B1MC подобны. Аналогично, так как CC1 - высота, треугольники ACC1 и C1MC также подобны.

5. В треугольнике ABB1: ∠ABB1 = ∠B1BD, и в треугольнике ACC1: ∠ACC1 = ∠C1CD.

6. Так как ∠B1BD = ∠C1CD и ∠B1BD = ∠ABB1, а ∠ACC1 = ∠C1CD, следовательно, ∠ABB1 = ∠ACC1.

7. Так как треугольники ABB1 и ACC1 подобны, то отношение длин сторон будет одинаковым: AB1 / AC1 = AB / AC.

8. AB1 = AB (так как BB1 - медиана, и медиана делит сторону пополам). Следовательно, AC1 = AC.

9. Так как AC1 = AC, треугольники ACC1 и ABC подобны.

10. Так как ∠ACC1 = ∠ABC и ∠ACC1 = ∠D, то ∠ABC = ∠D.

11. Так как ∠ABC = ∠D, и ∠ABC = 41° (как мы нашли в начале), то ∠D = 41°.

Теперь у нас есть значения углов A, B и C, а также угол D. Мы можем найти угол DMC, используя тот факт, что угол DMC = 180° - ∠B - ∠D: ∠DMC = 180° - 74° - 41° = 65°.

Итак, величина угла DMC равна 65°.