
Вопрос задан 01.05.2023 в 15:07.
Предмет Геометрия.
Спрашивает Нагаева Самира.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник ABC с прямым углом C.
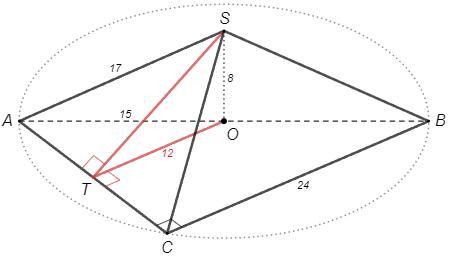
Основание высоты SO этой пирамиды является серединой ребра AB. а) Докажите, что SA = SC. б) Найдите угол между плоскостями SAC и ABC, если AB = 30, SC = 17, СB = 24.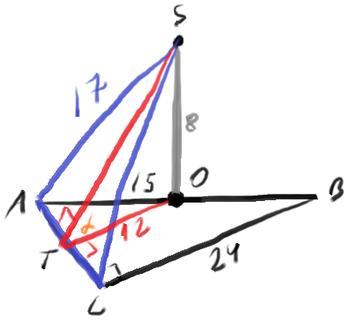
 0
0
 0
0
Ответы на вопрос
 Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.
Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.

Отвечает Евдокимова Таня.
Середина гипотенузы - центр описанной окружности.
Если вершина пирамиды падает в центр описанной окружности основания, то боковые ребра равны (SA=SC) и образуют с основанием равные углы.
(OA=OC, SO⊥OA, SO⊥OC, △SAO=△SCO по двум катетам)
Угол между плоскостями - угол между перпендикулярами к общей прямой.
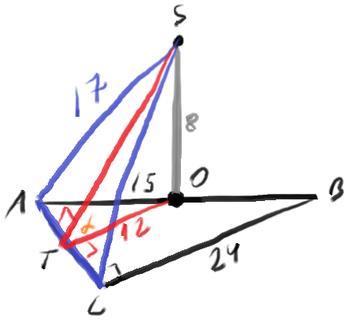
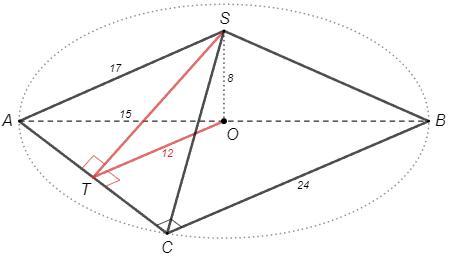
OT⊥AC, SO⊥(ABC) => ST⊥AC (т о трех перп)
∠STO - искомый
SO =√(SA^2-OA^2) =√(17^2-15^2) =8
OT =BC/2 =12 (OT||BC, средняя линия)
tg(STO) =SO/OT =8/12 =2/3
 0
0
 0
0
Топ вопросов за вчера в категории Геометрия
Последние заданные вопросы в категории Геометрия
Предметы
-
Математика
-
Литература
-
Алгебра
-
Русский язык
-
Геометрия
-
Английский язык
-
Химия
-
Физика
-
Биология
-
Другие предметы
-
История
-
Обществознание
-
Окружающий мир
-
География
-
Українська мова
-
Информатика
-
Українська література
-
Қазақ тiлi
-
Экономика
-
Музыка
-
Право
-
Беларуская мова
-
Французский язык
-
Немецкий язык
-
МХК
-
ОБЖ
-
Психология
-
Физкультура и спорт
-
Астрономия
-
Кыргыз тили
-
Оʻzbek tili





















