Question

Срочно!!! ЗАДАНИЕ 1 Докажите, что когда все двугранные углы при ребрах основания равны, то основание ее высоты – центр окружности, вписанной в основание пирамиды ЗАДАНИЕ 2 Площадь диагонального сечения правильной четырехугольной пирамиды в 2 раза меньше площади основания. Докажите, что ее противоположные ребра перпендикулярны.

Answer 1

ЗАДАНИЕ 1

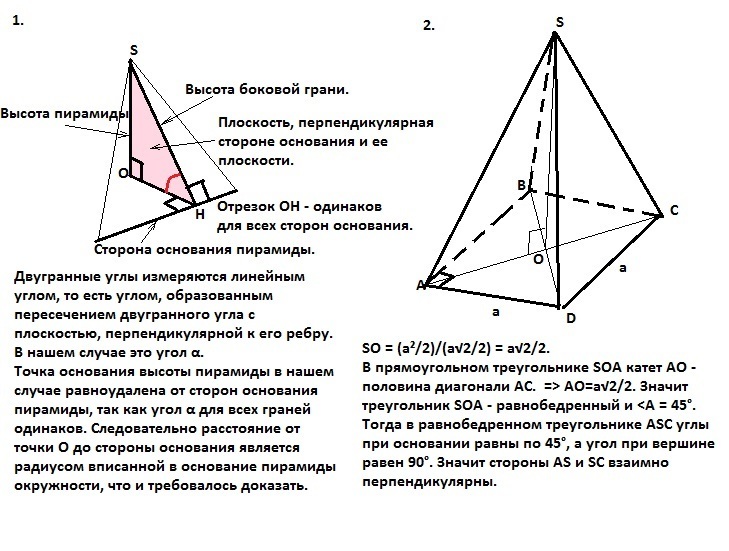
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру.  

Проведем через вершину пирамиды S плоскости, перпендикулярные ребрам двугранных углов пирамиды, то есть плоскости, перпендикулярные сторонам основания пирамиды и, следовательно, перпендикулярные самому основанию.

Тогда у всех этих плоскостей имеются две общие точки: вершина пирамиды S и ее проекция на основание пирамиды точка О. То есть эти плоскости пересекаются по прямой SO, являющейся высотой пирамиды. Линии пересечения этих плоскостей и пирамиды - это высота боковой грани и перпендикуляр из точки О основания высоты пирамиды к стороне основания пирамиды. Этот перпендикуляр - проекция высоты боковой грани на плоскость основания и в силу равенства двугранных углов (дано) одинаков для всех проведенных плоскостей, так как тангенс этих углов равен отношению высоты пирамиды к проекции высоты боковой грани. Итак, точка основания высоты пирамиды в нашем случае равноудалена от сторон основания пирамиды, следовательно, расстояние от этой точки до стороны основания пирамиды является радиусом вписанной в основание пирамиды окружности, что и требовалось доказать.  

ЗАДАНИЕ 2.

Основание правильной пирамиды SABCD - квадрат ABCD со стороной "а". Его площадь равна а². Значит площадь диагонального сечения равна а²/2 (дано). Диагональное сечение правильной пирамиды - равнобедренный треугольник ASC с основанием - диагональю квадрата, равной а√2. Площадь диагонального сечения S=(1/2)*АС*SO (SO - высота пирамиды). Итак, (1/2)*а√2*SO = а²/2. Тогда

SO = (а²/2)/(а√2/2) = a√2/2. В прямоугольном треугольнике SOA катет АО - половина диагонали АС.  АО=a√2/2. Значит треугольник SOA - равнобедренный и <A = 45°. Тогда в равнобедренном треугольнике ASC углы при основании равны по 45°, а угол при вершине равен 90°. Значит стороны AS и SC взаимно перпендикулярны.

AS и SC - противоположные ребра пирамиды. Они перпендикулярны. Что и требовалось доказать.

Answer 2

ЗАДАНИЕ 1: Для доказательства утверждения, что основание пирамиды является центром окружности, вписанной в основание, мы можем использовать следующие факты и свойства.

Предположим, что у нас есть пирамида с вершиной V и основанием ABCD, где углы при ребрах основания (углы ABC, BCD, CDA и DAB) равны между собой.

Шаг 1: Докажем, что точка O (центр окружности, вписанной в основание) лежит на пересечении биссектрис углов основания пирамиды.

• Поскольку углы при ребрах основания равны, то у них и их биссектрис равны между собой.
• Предположим, что биссектрисы углов ABC и CDA пересекаются в точке O.
• Также предположим, что биссектрисы углов BCD и DAB пересекаются также в точке O.
• По свойству биссектрисы каждый из углов при вершине V делится на два равных угла.
• Следовательно, точка O лежит на пересечении биссектрис углов основания пирамиды.

Шаг 2: Докажем, что точка O является центром окружности, вписанной в основание.

• Вспомним определение центра окружности, вписанной в четырехугольник. Центр окружности находится в точке пересечения биссектрис диагоналей четырехугольника.
• В нашем случае четырехугольником является основание пирамиды ABCD, и точка O является пересечением биссектрис его диагоналей.
• Значит, точка O является центром окружности, вписанной в основание пирамиды.

Таким образом, мы доказали, что когда все двугранные углы при ребрах основания пирамиды равны, то основание является центром окружности, вписанной в него.

ЗАДАНИЕ 2: Для доказательства утверждения, что противоположные ребра пирамиды перпендикулярны, если площадь диагонального сечения в 2 раза меньше площади основания, мы можем использовать следующие факты и свойства.

Пред