Question

В ящике находятся 10 деталей , изготовленных на 1-м станке, 8 деталей, изготовленных на 2-м станке и 12 деталей изготовленных на 3-м станке. Вероятность изготовления стандартной детали на 1-м станке равна 0,9, на 2-м 0,7, а на 3-м 0,8. Какова вероятность того , что наудачу извлеченная деталь стандартна? Какова вероятность того, что извлеченная деталь изготовлена на 1-м станке , если при проверке она оказалась стандартной ?

Answer 1

Всего 30 деталей.
Гипотезы:
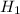$H_1$ - деталь изготовлена на первом станке
$H_2$ - деталь изготовлена на втором станке
$H_3$ - деталь изготовлена на третьем станке
Вероятности гипотез:
$P(H_1)=\frac{10}{30}=\frac13\\P(H_2)=\frac8{30}=\frac4{15}\\P(H_3)=\frac{12}{30}=\frac25$
Вероятность того, что деталь стандартная:
$P(A|H_1)=0,9\\P(A|H_2)=0,7\\P(A|H_3)=0,8$
Полная вероятность
$P(A)=P(A|H_1)\cdot P(H_1)+P(A|H_2)\cdot P(H_2)+P(A|H_3)\cdot P(H_3)=\\=0,9\cdot\frac13+0,7\cdot\frac4{15}+0,8\cdot\frac25\approx0,3+0,187+0,32=0,807$

Вероятность того, что наудачу взятая стандартная деталь произведена на первом станке
$P_A(H_1)=\frac{P(A|H_1)\cdot P(H_1)}{P(A)}=\frac{0,9\cdot\frac13}{0,807}=\frac{0,3}{0,807}\approx0,372$