Question

Помогите пожалуйста!!Вычислите угол между биссектрисой и медианой,проведёнными из прямого угла прямоугольного треугольника площадью 9/2 и гипотенузой 6

Answer 1

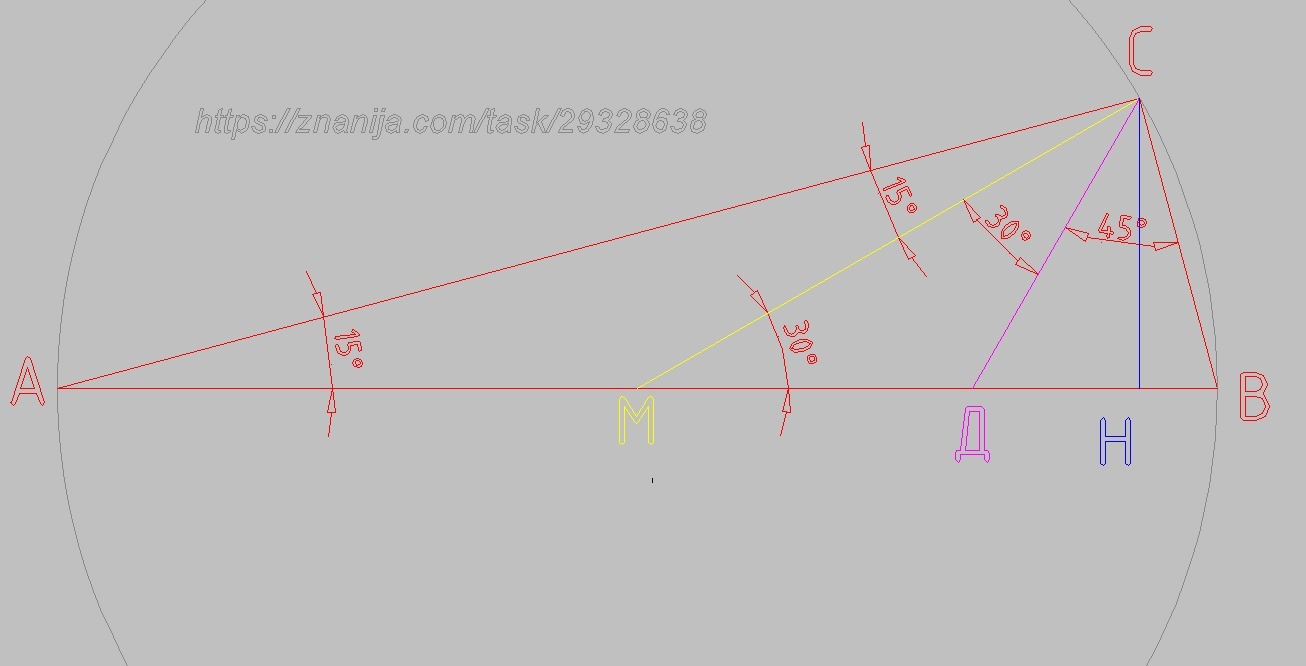
Гипотенуза АВ

АВ = 6

Высота СН

Медиана СМ

Площадь

S = 1/2*AB*CH = 9/2

1/2*AB*CH = 9/2

6*CH = 9

CH = 3/2

MB = МС = МА = 1/2*AB = 3

Площадь треугольника МСВ через сторону и высоту к ней

S(MCB) = 1/2*MB*CH = 1/2*3*3/2 = 9/4

Площадь треугольника МСВ через две стороны и угол меж ними

S(MCB) = 1/2*MB*MC*sin(∠CMB) = 1/2*3*3*sin(∠CMB) = 9/4

1/2*3*3*sin(∠CMB) = 9/4

sin(∠CMB) = 1/2

∠CMB = 30°

Опишем окружность вокруг ΔАВС

∠СМВ - центральный
∠САВ - вписанный, опирающийся на ту же дугу. И он в 2 раза меньше центрального

∠САВ = 30/2 = 15°
В ΔАМС
АМ = МС - треугольник равнобедренный
∠САМ = ∠АСМ = 15°
--------
СД - биссектриса, делит исходный угол в 90° пополам
∠ДСВ = 90/2 = 45°
-------
И теперь можно найти угол между биссектрисой и медианой

∠МСД = 90 - ∠АСМ - ∠ДСВ = 90 - 15 - 45 = 30°

Answer 2

∆ABC;<C=90°
CM медиан;СК биссектриса
АВ=6;S=9/2
<KCM=?
CM=AM=BM=6/2=3
∆CMB равнобед.<МСВ=<МВС
<МСК=<МСВ-<КСВ=<MCB-45°;(CK биссектриса;<<КСВ=90°:2=45°
АС=b;BC=a
a•b/2=9/2
a•b=9
a=6•sinA
b=6•cosA
6sinA•6cosA==9
sin2A=9/18=1/2
<2A=30°;<A=15°
<B=90°-15°=75°
<CMK=<MCB-45°=<MBC-45°=75°-45°=
30°

Answer 3

Чтобы вычислить угол между биссектрисой и медианой, проведёнными из прямого угла прямоугольного треугольника, нам понадобится некоторая геометрическая информация.

Известно, что площадь прямоугольного треугольника равна 9/2, а гипотенуза равна 6. Также, в прямоугольном треугольнике биссектриса из прямого угла является медианой, делящей гипотенузу на две равные части.

Мы можем использовать формулу для площади прямоугольного треугольника:

Площадь = (основание * высота) / 2.

Подставив известные значения, получим:

9/2 = (основание * высота) / 2.

Умножим обе части уравнения на 2, чтобы избавиться от знаменателя:

9 = основание * высота.

Так как основание - это гипотенуза треугольника, а высота - это расстояние от прямого угла до основания, получим:

9 = 6 * высота.

Делим обе части уравнения на 6:

9/6 = высота.

Высота треугольника равна 3/2.

Теперь, чтобы найти угол между биссектрисой и медианой, мы можем использовать геометрические свойства прямоугольного треугольника.

В прямоугольном треугольнике угол между биссектрисой и медианой, проведёнными из прямого угла, равен 45 градусам.

Таким образом, угол между биссектрисой и медианой равен 45 градусам.