
Вопрос задан 30.04.2023 в 13:58.
Предмет Геометрия.
Спрашивает Тащерский Ярик.
В треугольнике ABC проведенные медианы AN и BK пересекаются в точке M. Определи площадь
треугольника ABC, если площадь ABM равна 12 см2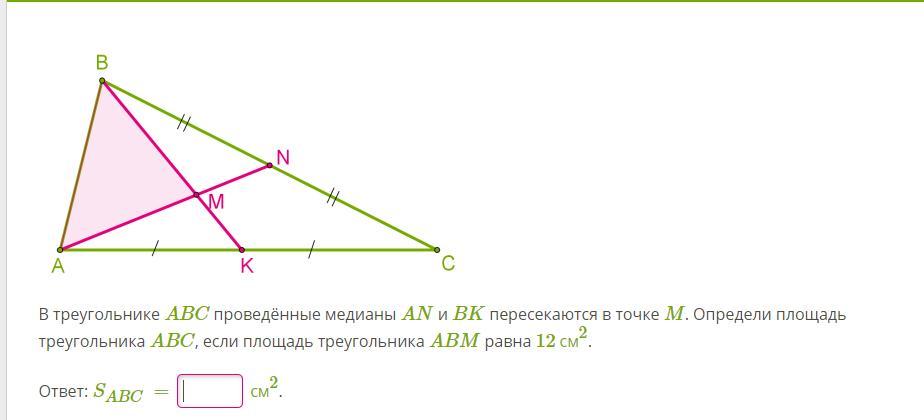
 0
0
 0
0
Ответы на вопрос
 Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.
Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.

Отвечает Бовкун Назар.
Ответ:36 cм²
Объяснение:
1) По свойству медиан любого треугольника они пересекаются и в точке пересечения делятся в отношении 2:1. ⇒Точка М делит АN в отношении 2:1, считая от А. т.е. АМ: МN=2:1
⇒ AM> MN в 2 раза.
2)Δ AMB и Δ BMN имеют одну и ту же высоту ( которую можно провести из вершины В на AN).
⇒ площадь S(ΔABM ) > S(Δ BMN) в два раза ( т.к. основание AM> MN в 2 раза) .
Значит S(Δ BMN) = 12:2=6 (см²)
3)S(Δ ABN)= S(ΔABM ) + S(Δ BMN) = 12+6=18 (см²)
4). Медиана любого треугольника делит его на два равновеликих треугольника. ⇒ S(Δ ABN)=S(Δ ANC)
S(Δ АBC)= 2·S(Δ ABN) =2·18=36 cм²
 0
0
 0
0
Топ вопросов за вчера в категории Геометрия
Последние заданные вопросы в категории Геометрия
Предметы
-
Математика
-
Литература
-
Алгебра
-
Русский язык
-
Геометрия
-
Английский язык
-
Химия
-
Физика
-
Биология
-
Другие предметы
-
История
-
Обществознание
-
Окружающий мир
-
География
-
Українська мова
-
Информатика
-
Українська література
-
Қазақ тiлi
-
Экономика
-
Музыка
-
Право
-
Беларуская мова
-
Французский язык
-
Немецкий язык
-
МХК
-
ОБЖ
-
Психология
-
Физкультура и спорт
-
Астрономия
-
Кыргыз тили
-
Оʻzbek tili















