
Вопрос задан 02.05.2023 в 16:13.
Предмет Геометрия.
Спрашивает Бирюкова Алеся.
С ЧЕРТЕЖОМ ! Плоскости альфа и бета перпендикулярны. Прямая L - линия их пересечения. В плоскости
альфа выбрали точку М, а в плоскости бета - точку N такие, что расстояния от них до прямой L равны 6 см и 7 см соответственно. Найдите расстояние между основаниями перпендикуляров, проведенных из точек М и N к прямой L, если расстояние между точками M и N равно √110 см .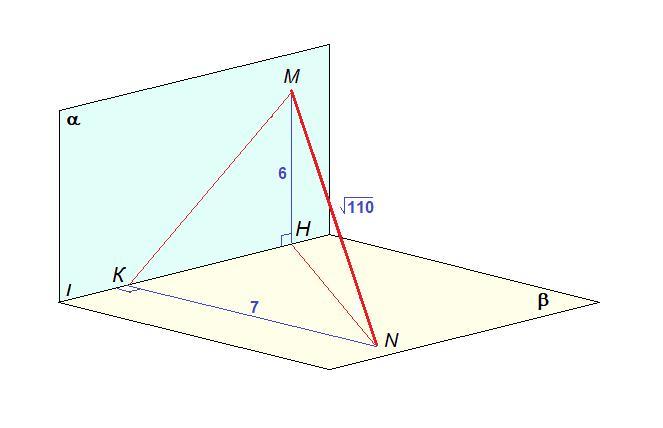
 0
0
 0
0
Ответы на вопрос
 Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.
Внимание! Ответы на вопросы дают живые люди. Они могут содержать ошибочную информацию, заблуждения, а также ответы могут быть сгенерированы нейросетями. Будьте внимательны. Если вы уверены, что ответ неверный, нажмите кнопку "Пожаловаться" под ответом.

Отвечает Князева Лиза.
Ответ:
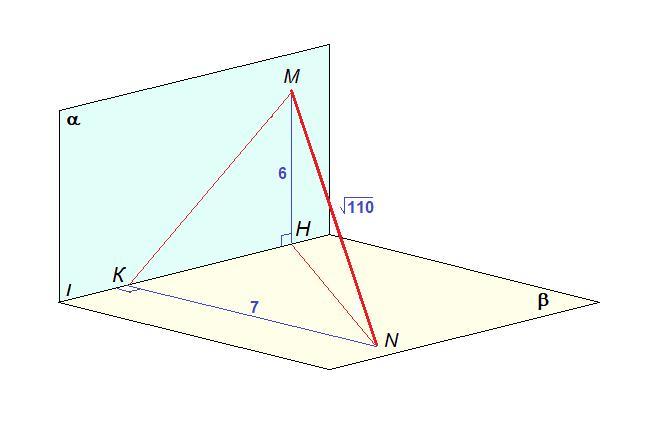
Расстояние между основаниями перпендикуляров к прямой равно 5 см.
Объяснение:
Проведем МН⊥ и NK⊥
.
МН = 6 см, NK = 7 см.
НК - искомое расстояние.
- Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная их линии пересечения, перпендикулярна другой плоскости.
Значит, MH⊥β, NK⊥α.
- Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.
Прямая NН лежит в плоскости β, значит МН⊥NH.
ΔMHN: ∠MHN = 90°, по теореме Пифагора
NH = √(MN² - MH²) = √(110 - 36) = √74 см
ΔNКН: ∠NКН = 90°, по теореме Пифагора,
HK = √(NH² - NK²) = √(74 - 49) = √25 = 5 см
 0
0
 0
0
Топ вопросов за вчера в категории Геометрия
Последние заданные вопросы в категории Геометрия
Предметы
-
Математика
-
Литература
-
Алгебра
-
Русский язык
-
Геометрия
-
Английский язык
-
Химия
-
Физика
-
Биология
-
Другие предметы
-
История
-
Обществознание
-
Окружающий мир
-
География
-
Українська мова
-
Информатика
-
Українська література
-
Қазақ тiлi
-
Экономика
-
Музыка
-
Право
-
Беларуская мова
-
Французский язык
-
Немецкий язык
-
МХК
-
ОБЖ
-
Психология
-
Физкультура и спорт
-
Астрономия
-
Кыргыз тили
-
Оʻzbek tili















